1.2 Neuronen – die Bausteine neuronaler Netze

Das menschliche Gehirn hat ca. 100 Milliarden Nervenzellen (auch Neuronen genannt), die als Bauteile der Informationsverarbeitung im Gehirn betrachtet werden können und ein wirklich sehr komplexes biologisches neuronales Netzwerk bilden. Doch was ist ein künstliches Neuron?

Ein künstliches Neuron ist ein kleines Stück Programmiercode, in dem versucht wird, die Funktionsweise eines biologischen Neurons stark vereinfacht in einer Programmiersprache nachzubauen. Oftmals wird zur besseren Veranschaulichung ein grafisches Modell gezeichnet, wie es auch weiter unten auf dieser Seite zu finden ist. Ein künstliches Neuron nimmt Eingaben (z. B. Zahlen) entgegen, verarbeitet sie mithilfe von mathematischen Operationen und gibt eine Ausgabe zurück. Die Ausgabe eines Neurons kann als Eingabe für ein anderes Neuron dienen, welches wiederum seine eigene Ausgabe generiert. Auf diese Weise arbeiten die Neuronen zusammen, um komplexe Muster und Zusammenhänge in Daten zu erkennen und Entscheidungen zu treffen.

Künstliche Neuronen sind echten biologischen Nervenzellen nur ganz grob und auf ganz einfache mathematische Weise nachempfunden. Obwohl das Thema Künstliche Intelligenz so schwierig erscheint, ist das künstliche Neuron als Baustein für neuronale Netze sehr einfach zu verstehen. Und dieselben künstlichen Neuronen, wie wir sie auf dieser Seite kennenlernen, werden auch in den kompliziertesten und größten künstlichen neuronalen Netzen eingesetzt.

Die ersten Überlegungen, künstliche Neuronen zu modellieren, sind über 80 Jahre alt, und erstaunlicherweise hat sich seitdem nur sehr wenig am Modell des künstlichen Neurons verändert. Heutzutage sind die Netze, zu denen diese zusammengeschaltet werden, allerdings sehr viel größer, das Internet hat massenhaft Trainingsdaten verfügbar gemacht und die Computer, auf denen solche Netze ausgeführt werden, sind deutlich schneller geworden.

Eine erste Annäherung

Man kann sich ein künstliches Neuron zunächst wie einen Lichtschalter vorstellen. Wenn das Neuron von genug Vorgängerneuronen aktiviert wird, feuert es, was am Beispiel des Lichtschalters das Licht anschalten wäre.

Man hat jedoch im Lauf der Zeit festgestellt, dass künstliche neuronale Netze viel besser funktionieren, wenn Neuronen nicht nur die beiden Zustände AN/AUS beherrschen, sondern wenn sie immer ein bisschen feuern. Je mehr sie aktiviert werden, desto mehr sollen sie feuern. Das kann man sich eher wie einen Dimmer-Lichtschalter vorstellen: Das Licht wird heller, je weiter man am Rad dreht. Feuern bedeutet in diesem Zusammenhang, dass das Neuron eine Zahl berechnet, die es an andere Neuronen weitergibt. Diese Zahl ist (analog zum Dimmer-Lichtschalter) größer, je mehr Vorgängerneuronen das künstliche Neuron aktiviert haben.

Das Modell eines künstlichen Neurons

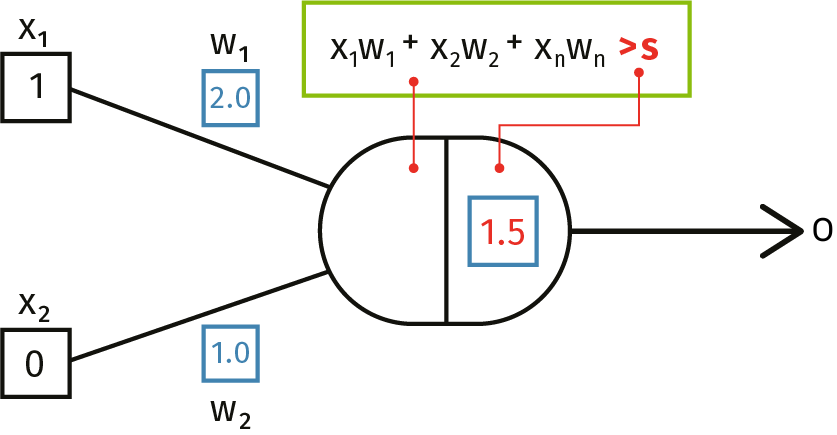
• Ein künstliches Neuron hat einen bis mehrere Eingänge, die als Eingaben bezeichnet werden, was mit dem Buchstaben x gekennzeichnet wird. Dabei werden alle Eingänge einfach von oben nach unten durchnummeriert: x1, x2, x3 usw. Es handelt sich dabei um Dezimalzahlen. Diese Zahlenwerte empfängt das Neuron entweder direkt oder es erhält sie von den Neuronen, die sich in der Schicht davor befinden.
• Jede Eingabe ist über ein veränderbares Gewicht mit dem Neuron verbunden. Dieses Gewicht soll die Stärke der Verbindung darstellen, denn man geht davon aus, dass eine solche Verbindung bei biologischen Neuronen stärker wird, je öfter sie benutzt wird. Dieses wird einfach durch eine Dezimalzahl dargestellt. Die Gewichte werden analog zur Eingabe mit dem Buchstaben w bezeichnet und ebenso durchnummeriert: w1, w2, w3 usw. Beachte: Die Gewichte werden während des Trainings verändert. 
• Das Neuron selbst ist in der Lage, seine Aktivierung zu berechnen, eine denkbar einfache Formel: Man summiert alle Produkte aus Eingabe und Gewicht paarweise auf, also: x1⋅w1 + x2⋅w2 + x3⋅w3 usw. In dem abgebildeten Beispiel kommt so eine Aktivierung von 2 zustande, denn 1⋅2 + 0⋅1 = 2.
• Neben der Aktivierung besitzt das Neuron einen veränderbaren Schwellwert, der mit dem Buchstaben s gekennzeichnet wird. Beim klassischen „Lichtschalter-Modell“ würde das Neuron nur feuern, wenn die Aktivierung des Neurons größer als der Schwellwert wäre (im abgebildeten Beispiel wäre dies der Fall). Bei der moderneren Variante ist es so, dass die Aktivierung und der Schwellwert in eine mathematische Formel einfließen, mit deren Hilfe die Ausgabe des Neurons berechnet wird. Diese Formel ist mit ein wenig Oberstufenmathematik ganz einfach zu verstehen und sehr simpel aufgebaut. Wichtig ist hier nur, dass dabei eine Dezimalzahl zwischen 0 und 1 herauskommt. Beachte: Der Schwellwert wird ebenso wie die Gewichte während des Trainings verändert.
• Jedes Neuron hat genau eine Ausgabe, um sein Signal (das „Feuern“) an andere verbundene Neuronen weiterzuleiten oder als Gesamtausgabe auszugeben. Die Ausgabe des Neurons wird in diesen Lerneinheiten mit dem Buchstaben o (wie Output) bezeichnet. Oftmals findet man in der Literatur auch den Buchstaben y. Darauf wurde hier jedoch verzichtet, um im weiteren Verlauf Verwechslungen zu vermeiden. 

Mehrere Neuronen bilden zusammen ein neuronales Netz. Üblicherweise werden Neuronen dabei in Schichten gruppiert und die Schichten werden miteinander verbunden. Neuronen sind nun nicht mehr einzeln, sondern im Verbund tätig. Die Ausgabe eines Neurons wird evtl. mit den Ausgaben anderer Neuronen zur Eingabe eines wieder anderen Neurons, dessen Ausgabe wiederum andere Neuronen aktivieren kann usw.

Doch die Gewichte und Schwellwerte eines neuronalen Netzes müssen nicht alle von Hand eingestellt werden. Sie werden alle mit zufälligen Zahlen erzeugt und dann hilft ein Algorithmus dabei, während des Trainingsprozesses die Gewichte und Schwellwerte der Neuronen so zu verändern, dass es am Ende möglichst gut funktioniert. Da das ganz schön viele Parameter sind, die optimal aufeinander abgestimmt werden müssen, ist das Training eines neuronalen Netzes oftmals sehr schwer nachzuvollziehen. Die folgenden Seiten sollen aber dabei helfen, ein Verständnis für den Begriff des Lernens bzw. Trainierens und den Begriff des Fehlers zu entwickeln. 

Ergänzung

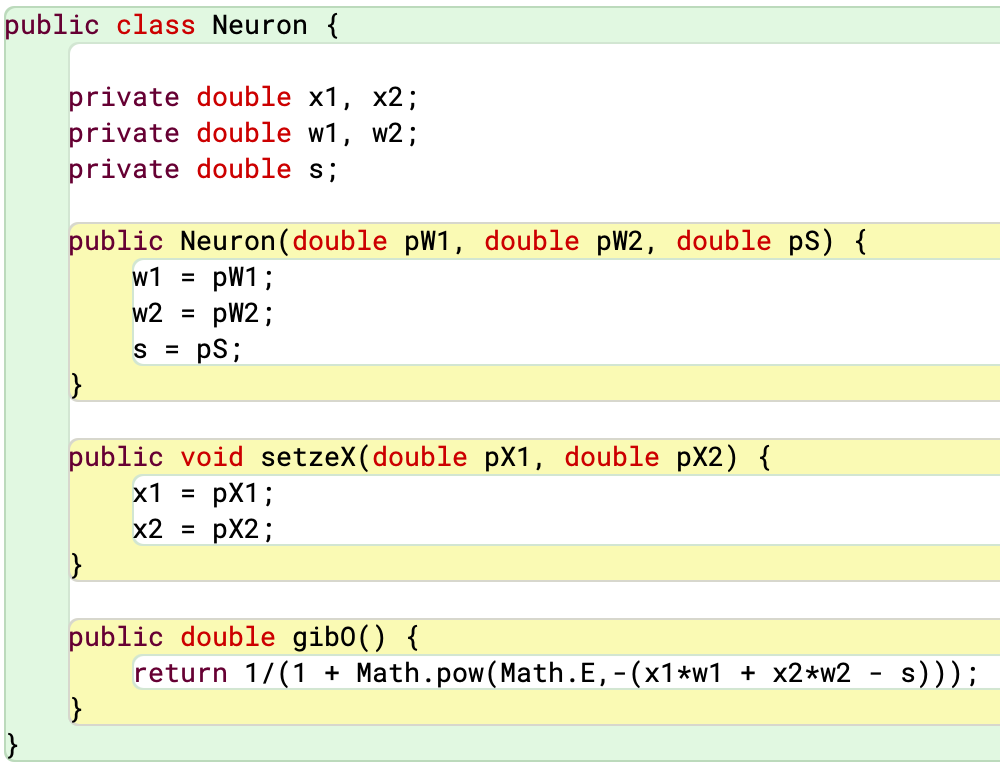
Um zu zeigen, dass in einem Neuron wirklich keine Magie steckt, und um eine bessere Vorstellung davon zu bekommen, wie man die grafische Abbildung des Neurons in Programmiercode umsetzt, zeigt die folgende Abbildung den Quelltext eines Neurons in der Programmiersprache Java. Selbst wer diese noch nicht kennt, kann vielleicht erahnen, dass hier keine höhere Intelligenz am Werk ist, sondern nur ein paar Zuweisungen und eine mathematische Berechnung. Insgesamt ist das erstaunlich wenig – auch wenn hier noch vernachlässigt wird, dass sich die Gewichte und Schwellwerte im Lauf der Zeit ändern können.