4.2 Fehler minimieren (einfach mit Hilfe)
In dieser Schwierigkeitsstufe trainiert man dasselbe Netz wie zuvor, es wird aber eine grafische Hilfe angeboten. Diese Hilfe ist etwas träge, da hier wirklich sehr viel berechnet werden muss; sie zeigt dafür aber den bestmöglichen Weg an, den man zur Fehlerminimierung einschlagen sollte, und hilft zusätzlich beim tieferen Verständnis des Optimierungsalgorithmus.
Den Fehler eines neuronalen Netzes verstehen
Wenn ein neuronales Netz nur ein einziges veränderbares Gewicht w hätte und sonst keinerlei Stellschrauben, an denen man drehen könnte, dann würden verschiedene Werte für das Gewicht w zu verschiedenen Fehlerwerten führen. Es gäbe aber sicherlich einen Wert, für den der Fehler am kleinsten wäre. In der folgenden Abbildung ist ein theoretisches Beispiel skizziert. So könnte der Fehler des Netzes in Abhängigkeit des Gewichtswerts w z. B. aussehen:
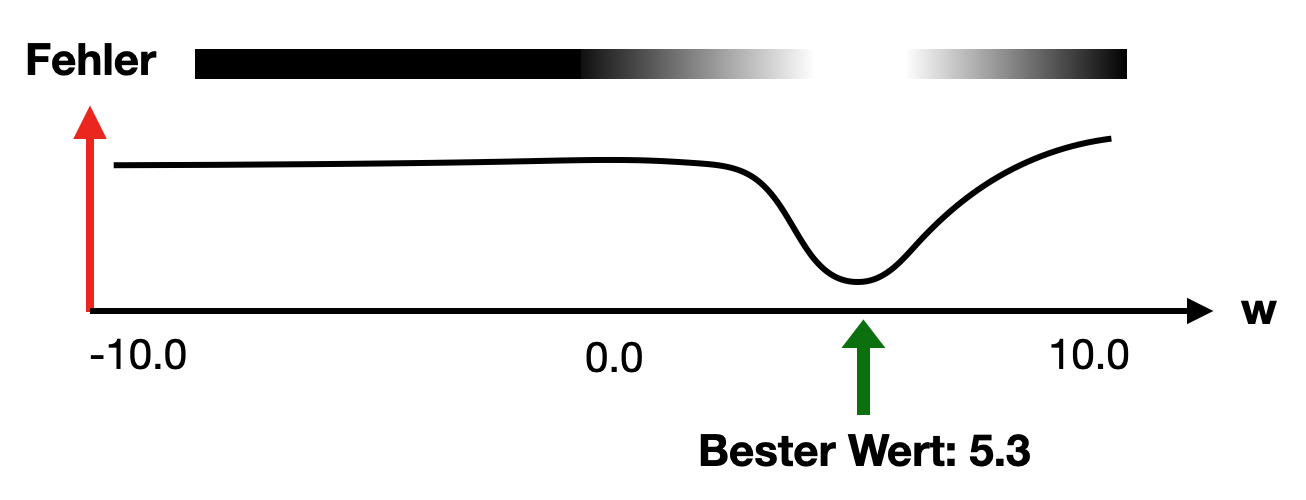
Möglicher Netzfehler bei einem Gewicht
Gäbe es jetzt noch ein zweites veränderbares Gewicht, dann wäre die Fehlerkurve schon schwieriger zu zeichnen, da es keine Kurve mehr wäre, sondern eine 3D-Fläche. Das Gewicht w1 spannt in der Abbildung die Achse nach links auf und das Gewicht w2 die Achse nach rechts-hinten. Den minimalen Fehler zu finden würde bedeuten, in das niedrigste Tal abzusteigen.
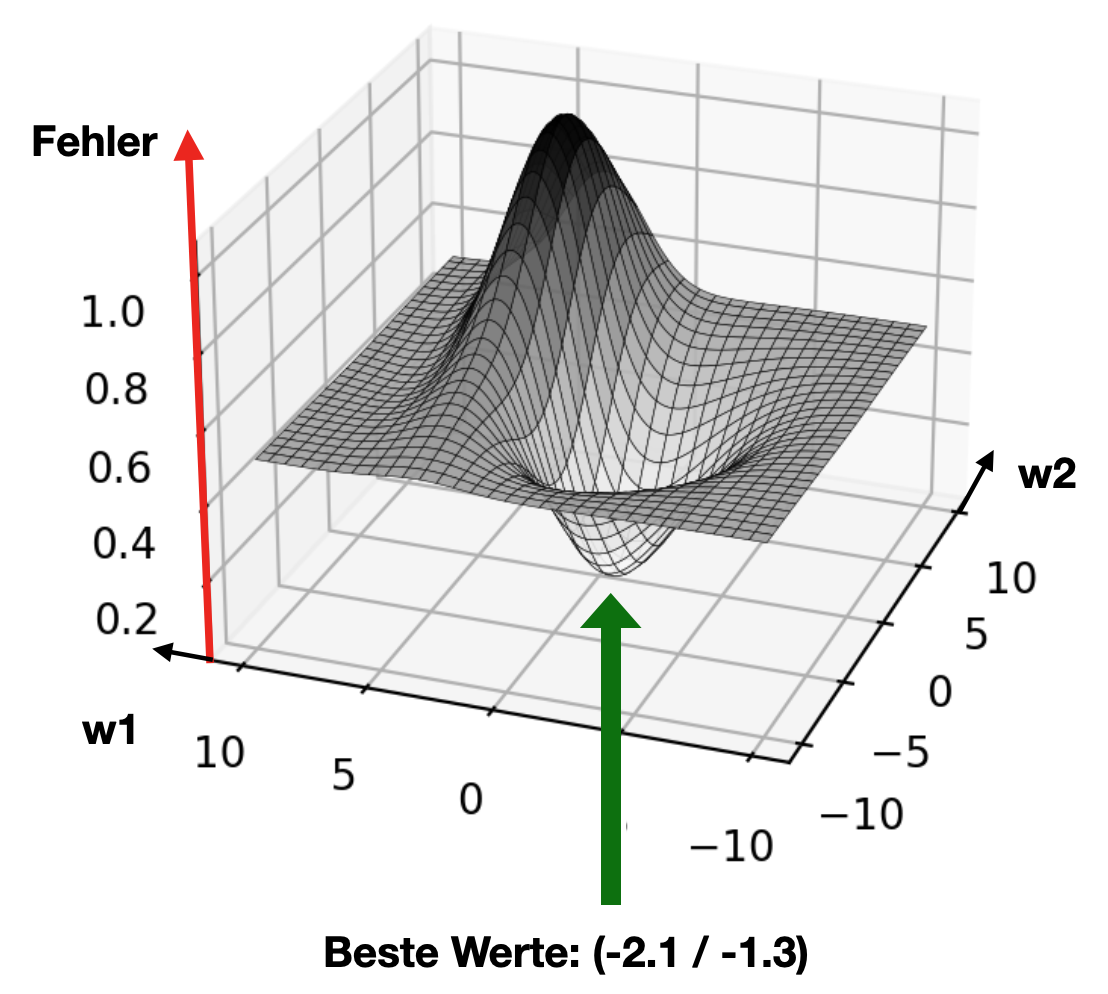
Möglicher Netzfehler bei zwei Gewichten
Bei diesem „Abstieg ins Tal“ kommt die Visualisierungshilfe ins Spiel. Das Ziel ist es immer, in den weißen Bereich der Täler zu kommen, da hier der Fehler kleiner ist. Die 3D-Landschaft wird uns dabei in der Hilfe immer von oben als 2D-Grafik gezeigt. Da das neuronale Netz in der Abbildung nicht nur zwei Gewichte, sondern auch noch einen Schwellwert hat, bietet es sich an, zunächst diesen zu ändern, um durch die dritte Dimension zu fahren und dann im Anschluss in den weißen Bereich zu navigieren.
Anleitung
- Wähle über die Checkboxen aus, welche Trainingsdaten geladen werden sollen.
- Klicke
Neu, um die voreingestellten Werte für eine einfache Trennung, eine neue zufällig gewählte Boolesche Funktion oder neue Zufallszahlen als Datensatz zu wählen. - Klicke nun auf die Plus- oder Minus-Zeichen in der Abbildung, um die Gewichte oder den Schwellwert zu ändern. Es wird automatisch der aktuelle Fehler des Netzes angezeigt. Ist der Fehler klein genug, erhältst du einen Hinweis mit deiner benötigten Zeit. Steuere über die Plus- oder Minus-Zeichen den kleinen schwarzen Kreis innerhalb der grafischen Hilfe in einen möglichst weißen Bereich. Es kann passieren, dass der Bereich für die Beispieldaten mit den Zufallszahlen nicht ausreicht.
- Klicke
Reset, um alle deine aktuellen Änderungen an den Gewichten und am Schwellwert wieder rückgängig zu machen. - Klicke
Train, um das Training zu starten oder wieder aufzunehmen. - Blau steht in der Abbildung links für negative Werte und rot für positive Werte.
Aufgabe
Probiere viele verschiedene Beispiele aus und minimiere jeweils den Fehler des Netzes.
Aus der algorithmischen Sichtweise
Bei allen auf diesen Seiten verwendeten neuronalen Netzen werden beim Training die Verfahren Backpropagation und Gradient Descent eingesetzt. Diese verfolgen eine ganz eigene, recht komplizierte Strategie, den Fehler von hinten nach vorne (also zurück, daher „Backpropagation“) auszumerzen. Die Gewichte werden schichtweise (von der Ausgabe zur Eingabe) abhängig von ihrem Einfluss auf den Fehler des Netzes geändert. Rein algorithmisch wird dabei ebenso versucht, möglichst weit „in Täler abzusteigen“ (dafür gibt es tatsächlich rein mathematische Lösungsverfahren). Allerdings wäre das Bild mit dem Tal nur im dreidimensionalen Fall wirklich anschaulich, wenn das gesamte neuronale Netz nur zwei Gewichte hätte. Für jedes weitere Gewicht und jeden weiteren Schwellwert kommt nämlich eine Dimension dazu. Wenn neuronale Netze mit zigtausend Neuronen trainiert werden, bedeutet das, dass auch hier ein möglichst tiefes Tal in einem Raum mit zigtausend Dimensionen gefunden werden muss, was man sich allerdings gar nicht mehr vorstellen kann. Algorithmisch lösen lässt es sich trotzdem – dank moderner PC-Hardware sogar sehr schnell.
Um besser zu verstehen, wie schwierig es bereits ist, 13 verschiedene Parameter (also Gewichte, Schwellwerte) aufeinander abzustimmen, sollte man unbedingt das schwierigere Beispiel auf der nächsten Seite ausprobieren!
Diese Seite teilen

